Understanding Bitcoin Private Key Coordinates on the ECC Curve

Introduction

The Elliptic Curve Digital Signature Algorithm (ECDSA) is widely used for secure transactions on the Ethereum blockchain. One of the key components of ECDSA is the private key, which is a crucial component for verifying and signing digital signatures. However, there is an interesting aspect to consider when it comes to Bitcoin, where the private key is supposedly represented as x,y coordinates on an elliptic curve.

The Elliptic Curve Representation

In ECDSA, the private key is usually represented using a set of (x,y) coordinates on an elliptic curve. This representation allows for efficient and secure calculations involving the private key. However, it is essential to note that this coordinate system is not directly applicable to Bitcoin.

Are integer x,y coordinates the private key?

One might assume that if the private key were a single point on an elliptic curve (x,y), it could be represented as x,y coordinates in ECDSA. However, this assumption is not true for several reasons:

–
Integer nature

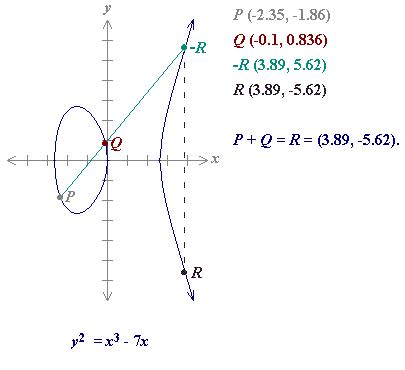
: The Bitcoin private key is in fact an integer, meaning it can only have two possible values: 0 or 1.

–
Binary representation: The binary representation of the private key is also a single integer (usually represented as 32 bits). In binary, this represents a very specific set of digits that cannot be represented by x,y coordinates on an elliptic curve.

Conclusion

While the idea of ​​representing Bitcoin private keys using x,y coordinates may seem intriguing, it is not precise. The integer representation of the private key is in fact related to binary digits, which are also single-coordinate points (x,y) on an elliptic curve. This highlights another aspect of how ECDSA and Bitcoin differ in their use of cryptographic primitives.

References

– [ECDSA algorithm documentation](

– [Bitcoin private key representation](